tdunning commented on pull request #7069: URL: https://github.com/apache/incubator-pinot/pull/7069#issuecomment-864294396
Errors in estimation with the t-digest are usually phrased in terms of quantile error (that is, q, not the samples x). Errors in the sample space are notionally unbounded because the sample distribution can be stretched. In addition, t-digest is normally used when estimating tails of a distribution so the relative error $\Delta q$ / \max(q, 1-q)$ is controlled rather than the absolute error. The result is that error near the median can be orders of magnitude larger than near the extremes. For uniform distribution, errors in sample space are the same as errors in quantile (subject to scaling by the range). Regarding error scaling with respect to $q$, the figure below shows that for small values of $\delta$ errors scale roughly with $1/\delta^2$ and then transitions to scaling roughly with $1/\sqrt(\delta)$ ([see this article on t-digest](https://www.sciencedirect.com/science/article/pii/S2665963820300403) for more detailed information). The problem with this statement is that it doesn't really respond to your question because it is, again, focused on extreme $q$.  Errors near the median for well-behaved distributions like the uniform distribution should be roughly like $2/\delta$ given that there should be about $\delta/2$ centroids. The actual results will be somewhat better than this to the extent that interpolation works. Here is a figure that shows max error of quantile(x) for selected values of x at various combinations of delta and number of samples. Note that these errors are relative to the exact empirical quantiles. Errors in consistency between different t-digests could, conceivably, be double these numbers. Also, if you looked at a high resolution scan of possible values of x, you would likely find bad cases right at the transition between 1 and 2 samples per centroid. 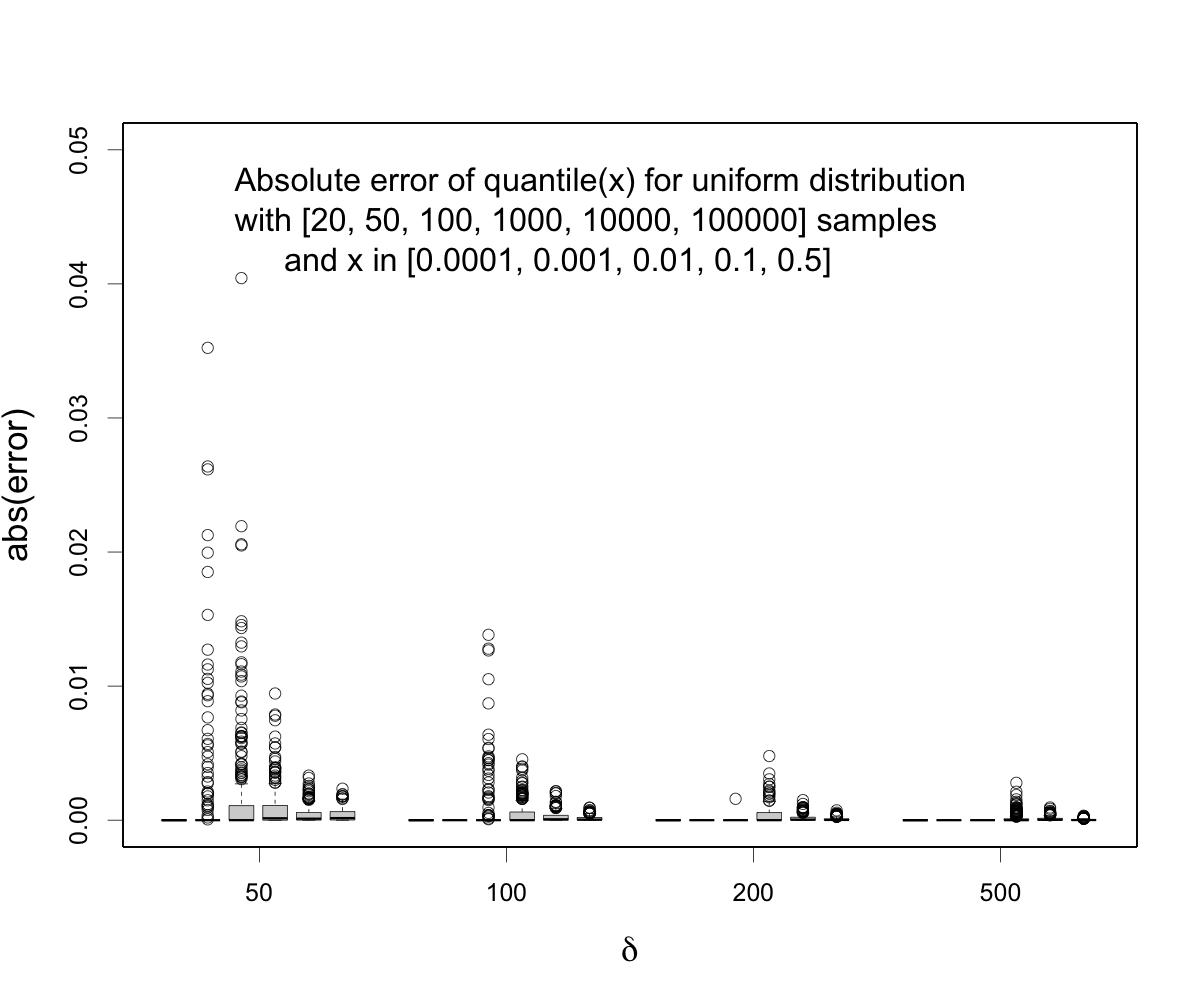 Basically, $\delta=100$ has *lots* fewer outlier cases and is likely to be what you need. I note that this is the default value for most of your code. This particular test stands out a bit for using $\delta = 50$. This last figure is generated from the file `median-error.csv` produced by the `com.tdunning.tdigest.quality.CompareKllTest#testMedianErrorVersusScale` test in the main branch of t-digest. The code to produce the [figure can be found in this gist](https://gist.github.com/tdunning/78a4a8ee17b48d35cd7ec496b2f0d817). -- This is an automated message from the Apache Git Service. To respond to the message, please log on to GitHub and use the URL above to go to the specific comment. For queries about this service, please contact Infrastructure at: us...@infra.apache.org --------------------------------------------------------------------- To unsubscribe, e-mail: commits-unsubscr...@pinot.apache.org For additional commands, e-mail: commits-h...@pinot.apache.org
